gestión del tiempo | gestionproyectos

La Gestión del Valor Ganado (EVM ®) es una de las técnicas más difundidas para el seguimiento y control de proyectos que debemos conocer y tener la posibilidad de aplicar. También es una de las áreas temáticas más importantes del examen de certificación PMP®.

En cualquier proyecto de la clase que sea, las tres variables de alcance, tiempo y costo están siendo constantemente cuestionadas e influenciadas por factores tanto internos como externos al proyecto. Surgen frecuentes cambios en los requisitos y por lo tanto en el alcance, en la calidad, en el plan de ejecución y en los costos que integran el presupuesto.

Con EVM ®, a fecha de estado durante el seguimiento de un proyecto podremos responder a tres preguntas clave:

El objetivo con la Gestión del Valor Ganado, es evaluar y cuantificar en el nivel de gestión deseable (cuenta de control) los siguientes valores e indicadores clave de desempeño que permiten conocer tanto el estado actual del proyecto, como también pronosticar el posible estado final de nuestro proyecto:

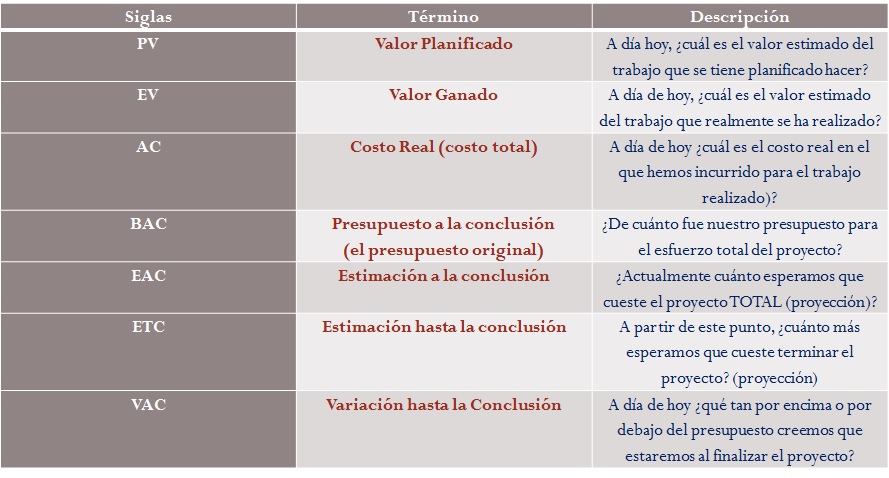
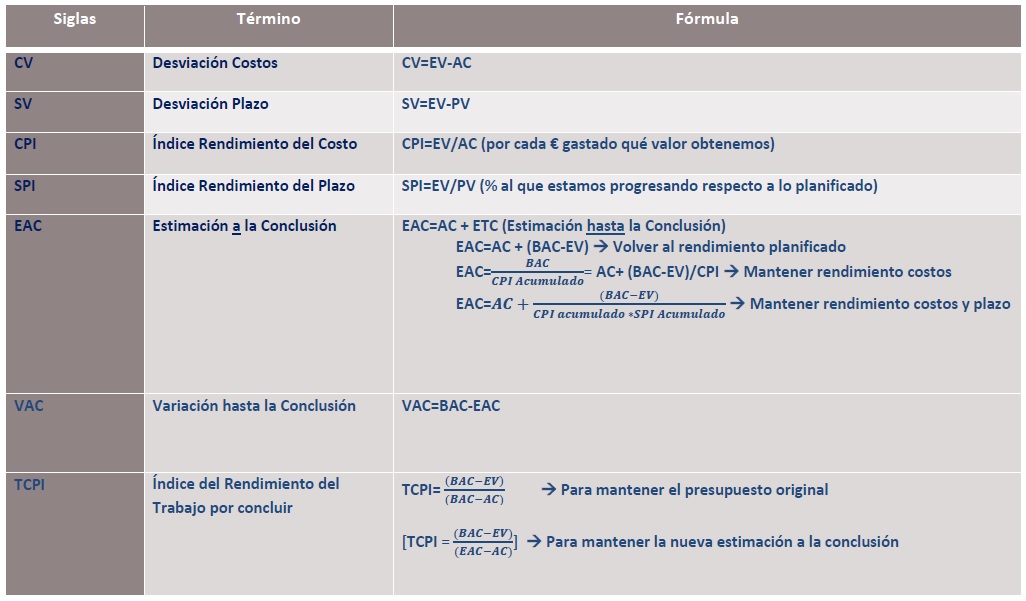
Vamos a describir un ejemplo sencillo:

Nos encargan el siguiente proyecto: vallar una finca de forma cuadrada, con 4.000m de perímetro, es decir, 1.000m cada lado:

La planificación que realizamos como directores de este proyecto es la siguiente: completaremos el vallado en 4 días con un presupuesto de 4.000€, según lo siguiente:

Día 1 Día 2 Día 3 Día 4

1.000m/1.000€ 1.000m/1.000€ 1.000m/1.000€ 1.000m/1.000€

1.000m/1.000€ 750m/1.200€ 750m/1.000€

100% 75% 75%

El día 1 marcha según lo planificado, es decir, vallamos 1.000m y nos hemos gastado 1.000€; el día 2 marcha encontramos unas piedras que no habíamos previsto y solo avanzamos el 75% de lo planeado y, además, a un coste de 1.200€, ya que hemos tenido que traer maquinaria para quitar las piedras, y el día 3 volvemos a encontrar piedras, por lo que de nuevo sólo avanzamos el 75% según lo planeado a un coste de 1.000€, ya que la maquinaria ya estaba allí del día anterior. Por lo tanto, al final del tercer día, el avance es el marcado en rojo en la tabla de arriba.

El cliente nos pregunta que, ante estos sucesos imprevistos, ¿cuánto será la estimación del presupuesto a la finalización de las obras el 4º día?

Tenemos los siguientes datos al final del día 3:

Valor Planificado/Planned Value = 3.000€ (1000+1000+1000)
Coste Real/Actual Cost = 3.200€ (1.000+1.200+1.000)
Valor Ganado/Earned Value = 2.500€ (1.000+750+750)

Y según esos datos, las variaciones son las siguientes:

SV (Variación del cronograma/Schedule Variance) = EV-PV = 2.500-3.000 = -500€
CV (Variación del coste/Cost Variance) = EV-AC = 2.500-3.200 = -700€

Además, podemos conocer los índices del rendimiento tanto del cronograma como del coste:

SPI (Índice del Rendimiento del Cronograma/Schedule Performance Index)
- SPI = EV/PV = 2.500/3.000 = 0,83. Estamos progresando al 83% del ritmo originalmente planificado.

CPI (Índice del Rendimiento del Coste/Cost Performance Index)
- CPI = EV/AC = 2.500/3.200 = 0,78. Estamos obteniendo un valor de 0,78€ por cada 1€ que estamos gastando en el proyecto.

Con los datos anteriores, el cliente nos pregunta cuánto será el presupuesto final, para lo cual calculamos varios EAC basado en las hipótesis sobre el desempeño hasta la fecha (Estimación a la conclusión/Estimation at completion):

Que el 4º día no encontremos más piedras, es decir, que no existirá variabilidad ni del coste ni del plazo y volvamos al ritmo originalmente planificado:

EAC = AC+(BAC-EV) ; EAC = 3.200+(4.000-2.500); EAC = 4.700€

BAC = presupuesto a la finalización/budget at completion

Que el 4º día nos vamos a encontrar con los mismos problemas, es decir, que la variabilidad del coste y del plazo será la misma que hasta la fecha actual:

EAC = AC+[(BAC-EV)/(CPI*SPI)] ; EAC = 3.200+[(4.000-2.500)/(0,83*0,78)] = 4.738,46€

NUEVA CONVOCATORIA DEL CURSO ONLINE DE PREPARACIÓN PARA LA CERTIFICACIÓN PMP®

¡Solicita Información e Inscríbete!

En la siguiente pregunta ejemplo de examen test de la certificación PMP^®, se plantea un diagrama de red, las secuencia de relaciones lógicas entre las actividades y la cuestión sobre el inicio temprano (lo antes que puede comenzar una actividad) de la actividad J, y un relación de dependencia con predecesora (SS: Inicio-Inicio) diferente a la más común (FS: Final-Inicio):

En rojo describimos el recorrido por el diagrama de red de izquierda a derecha de los diferentes camino lógicos de la red que permite calcular el Inicio temprano (ES) y el Fin temprano (EF) de cada actividad.
Comentamos únicamente las que tienen relaciones con adelantos/retrasos diferentes a la estándar FS: Final-Inicio =>una actividad sucesora no puede iniciarse hasta que la predecesora haya finalizado:

B–> H (FS-2): Sin el adelanto de dos días, H tendría ES(H)=7 y EF(H)= 15. Como se aplica ese adelanto ES(H)= 5 y EF (H)=13
G–> K (FS 4): Sin el retraso de 4 días, K tendría ES(K) = 14 y EF(K)= 15. Cuidado aquí porque como hay 3 predecesoras (H,J y G) aplicamos la regla de que el ES de la sucesora es el EF (fin temprano) más tardío de las predecesoras (+1 día por estar incluyendo en las «cuentas» el ultimo día en los EFs), de esta forma mantenemos la coherencia de la relación lógica entre actividades (predecesora-sucesora). Con el retraso de los 4 días en G, el EF más tardío pasa a ser justamente el de esta actividad (14)=> ES(K)=15 y EF (K) =16
Para J, tenemos dos predecesoras y aunque hay una relación SS (inicio-inicio: una actividad sucesora no puede iniciar hasta que la predecesora haya iniciado) con F, para seguir manteniendo la coherencia de las relaciones lógicas entre las actividades, el ES de J seria el EF más tardío de las predecesoras => ES(J)= 8 y EF(J) =13

NOTA: Si J solo tuviera como predecesora a F, SÍ que deberíamos haber forzado a que su ES(J)=5 y por lo tanto su EF(J) =10 para mantener la relación SS.

Para el camino de vuelta través del diagrama de red, en verde, calculamos el Inicio tardío (LS) y el Fin tardío (LF) de cada actividad:

Para G, volvemos a aplicar el retraso de 4 días (con cuidado porque estamos recorriendo el camino a la inversa), esto es, sin el retraso para G LF(G)=14, con la retraso de 4 días y teniendo en cuenta que la relación es FS (Final-Inicio)=> LF(G) =10 y LS(G)=5
Para B (es la única predecesora de H), sin el adelanto LF(B)=5, Como B tiene una relación FS con H y un adelanto de 2 días (H debe iniciar cuando B finaliza – 2 días)=> LF(B)=7 y LS(B)=3
En el caso de F (solo tiene una sucesora J y una relación SS con ella)=> si fuera una relación estándar FS(Final-Inicio) entonces LF(F)=8 y LS(F)=7 pero como la relación es SS, debemos forzar a que el LS(F) sea el LS(J)=> LS(F)=9 y por lo tanto LF(F) =10.